Question

Find the values of my and n ​

Answer 1

`{ \boxed{ \bold{ \tt{ \: m \: = \: 60 \degree \:, n \: = \: 24 \degree}}}}`

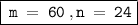
Last option is correct.

Explanation:

`{ \text{First, \: let's \: know \: about \: corresponding \: angles}}:`

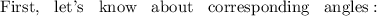
Corresponding Angles :

A pair of interior and exterior angles which lies to the same side of the transversal is called corresponding angles. The lines make an F - shape. In our case , 2m° and ( 4m - 120) ° are corresponding angles. Also, Remember that corresponding angles are always equal. Now, Let's create an equation and solve for m.

`\rm \: { \: 2m = 4m - 120}`

⇢
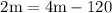
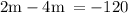`\rm{2m - 4m \: = - 120}` { Move 4m to left hand side and change it's sign}

⇢
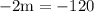`\rm{ - 2m = - 120}` { Subtract 4m from 2m}

⇢
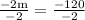`\rm{ ( - 2m)/( - 2) = ( - 120)/( - 2)}` { Divide both sides by -2}

⇢
`\rm{ m = 60 \degree}`

`\text{Now, \: Let's \: know \: about \: vertically \: opposite \: angles} :`

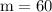
Vertically opposite angles :

When two lines intersect, the angles formed opposite to each other are called vertically opposite angles. In our case, ( 4m - 120 )° and 5n° are vertically opposite angles. Vertically opposite angles are always equal. Now, Let's create an equation and solve for m.

We have , m = 60°

`\rm{5n = 4m - 120}`

⇢
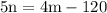
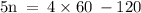`\rm{5n \: = \: 4 * 60 \: - 120}` { Plug the value of m}

⇢
`\rm{5n = 240 - 120}` { Multiply the numbers : 4 by 60 }

⇢
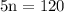`\rm{5n = 120}` { Subtract 120 from 240 }

⇢
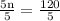`\rm{ (5n)/(5) = (120)/(5) }` { Divide both sides by 5 }

⇢
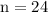
`\rm{n = 24 \degree}`

`\text{Hope \: I \: helped}`!

`\text{Best \: regards}` !

~
`\text{TheAnimeGirl}`

Answer 2

m=60 and n=24

Explanation:

Corresponding Angles:

2m = 4m - 120

-2m = -120

m = 60

Vertical Angles:

4m - 120 = 5n

4(60) - 120 = 5n

240 - 120 = 5n

120 = 5n

5n = 120

n = 24

(This is what I got, I apologize if I'm incorrect)