Answer:
D) 2
Explanation:
First Method: Solve for x
There are two ways to find what value of x will make this equation true. The first method is to solve for x in the equation.
The given equation is:
Rewrite this equation by evaluating the exponent on the right side of the equation, and make 4 * x = 4x.
Subtract
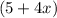 from both sides of the equation (so we can keep the
from both sides of the equation (so we can keep the
 positive). It's just preference.
positive). It's just preference.
Simplify the right side of the equation by combining like terms and rearranging terms to follow the format of
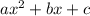 .
.
Factor this quadratic by seeing what two terms multiply to
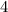 and add up to
and add up to
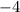 . These two terms are
. These two terms are
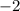 . Notice that this is a perfect square.
. Notice that this is a perfect square.
Solve for x by setting the expressions inside the parentheses equal to 0.
This means that answer choice D) 2 is correct.
Second Method: Plug in the answer choices
The second method is to substitute the given answer choices into the equation, which works when you are given answer choices. Otherwise, the first method is ideal.
Use the form of the equation where we set all the terms equal to 0.
Start with answer choice A, and work your way up to D to check all of them.
A) Substitute 5 for x into the equation.
This is a false statement; 0 does not equal 1.
B) Substitute 4 for x into the equation.
This is a false statement; 0 does not equal 4.
C) Substitute 3 for x into the equation.
This is a false statement; 0 does not equal 1.
D) Substitute 2 for x into the equation.
This is a TRUE statement; thus, the answer is D) 2.