Question

In an isosceles triangle the length of the legs is 8 cm and the angle between them is 150°. Find the altitude to the legs and the area of the triangle.

Find AH and Aᴬᴮᶜ

Answer 1

AH = 4 units

Area of ΔABC = 16 square units

Explanation:

Since ΔABC is an isosceles triangle,

AC = BC

∠CAB ≅ ∠ABC [Opposite angles of the equal sides in a triangle are equal]

In ΔABC,

m∠CAB + m∠ABC + m∠ACB = 180°

m∠ABC + m∠ABC + 150° = 180°

2m∠ABC = 30°

m∠ABC = 15°

Now we apply cosine rule in ΔABC,

AB² = AC² + BC² - 2(AB)(BC)cos(m∠ACB)

AB² = 8² + 8² - 2(8)(8)cos(150°)

AB² = 128 + 110.85

AB =
`√(238.85)`

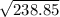
AB = 15.45

In ΔABH,

sin(m∠ABH) =
`(AH)/(AB)`

sin(15°) =
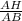
`(AH)/(15.45)`

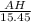
AH = 15.45sin(15°)

AH = 3.998

AH ≈ 4.0 units

HC =
`\sqrt{8^(2)-4^2}`

=
`√(48)`

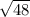
= 6.93

Area of the triangle ABC =
`(1)/(2)(BC)(AH)`

=
`(1)/(2)(8)(4)`

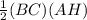
= 16 square units