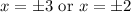Answer:
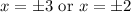
Explanation:
We have the equation:
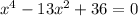
Notice that this resembles a quadratic. So, we can use u-substitution to solve for the values of x.
Let
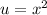 . Then:
. Then:
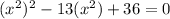
Perform the substitution:
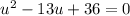
We can now factor using -9 and -4:
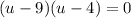
Zero Product Property:
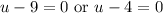
Solve for each case:
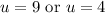
Substitute back u:
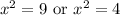
Take the square root of both sides for both equations. Since we’re taking an even root, we will need plus/minus. Therefore, our possible values of x are: