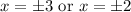Question

Solve using u for all possible values of x.

`x^(4)-13x^(2)+36=0`

Answer 1

`x=\pm3\text{ or }x=\pm2`

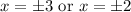
Explanation:

We have the equation:

`x^4-13x^2+36=0`

Notice that this resembles a quadratic. So, we can use u-substitution to solve for the values of x.

Let
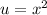`u=x^2`. Then:

`(x^2)^2-13(x^2)+36=0`

Perform the substitution:

`u^2-13u+36=0`

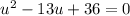
We can now factor using -9 and -4:

`(u-9)(u-4)=0`

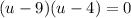
Zero Product Property:

`u-9=0\text{ or } u-4=0`

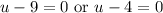
Solve for each case:

`u=9\text{ or } u=4`

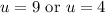
Substitute back u:

`x^2=9\text{ or } x^2=4`

Take the square root of both sides for both equations. Since we’re taking an even root, we will need plus/minus. Therefore, our possible values of x are:

`x=\pm3\text{ or }x=\pm2`