Given:
The composition of the translations is
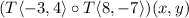
To find:
The composition of the translations in one translations.
Solution:
We know that,
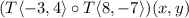 means
means
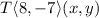 is followed by
is followed by
 .
.
In
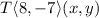 ,
,
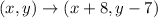
So,
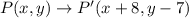 .
.
In
 ,
,
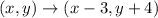

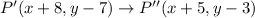
Now, after composition of the translations
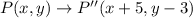
Here, rule of translation is
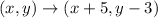
Therefore, rule of translation is
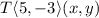 .
.