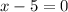Question

Write an equation in standard form for the line that passes through the given points

(5, -3) and (5,6)

Answer 1

`x=5`

Explanation:

The standard form for equation of the line is
`Ax + By = C \\`

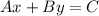
We first find the slope of the line:

Slope, m is given by:

`{\displaystyle {\Delta y\over \Delta x}={y_1-y_2\over x_1-x_2}}`

`{\displaystyle m={-3-6\over 5-5}={-8\over 0}=\infty}`

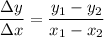
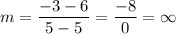
This means that the slope is undefined.

And that the line is perpendicular to the x-axis and parallel to the y -axis.

Being that the line is parallel to the y-axis it means that the line intersect at no point with the y-axis so our equation is solved as follows:

Pick any point
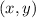`(x,y)`along the line and one of the known points, say,
`(5,6)`

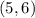
So in solving for m,

we find that :

`{\displaystyle {y_1-y_2\over x_1-x_2}={y-6\over x-5}={-8\over 0}}`

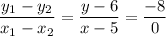
Cross multiplication gives us:

`0(y-6)=-8(x-5)`

`-8(x-5)=0`

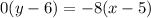
Dividing through by
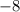`-8` , we get:

`x-5=0`

`x=5`