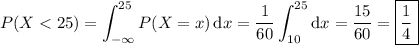Question

Suppose x is a random variable best described by a uniform probability distribution with c = 10 and d = 70. Find P(x < 25).

Answer 1

If you're talking about a discrete distribution, then

`P(X=x)=\begin{cases}\frac1{61}&\text{for }x\in\{10,11,12,\ldots,70\}\\0&\text{otherwise}\end{cases}`

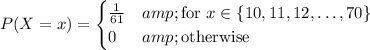
(1/61 because there are 61 numbers in the range of integers from 10 to 70) so that

`P(X<25)=\displaystyle\sum_(x=10)^(24)P(X=x)=\boxed{(15)/(61)}`

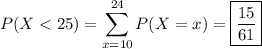
If the distribution is continuous, we would have the same density function, but x can be any real number in the interval [10, 70]. So we have

`P(X<25)=\displaystyle\int_(-\infty)^(25)P(X=x)\,\mathrm dx=\frac1{60}\int_(10)^(25)\mathrm dx=(15)/(60)=\boxed{\frac14}`