Answer:
Point-slope form:
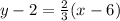
y-intercept form:
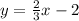
Explanation:
To find the equation of a parallel line through a point, we can use the point-slope form as our basis. To do this, we need the coordinates of a point on the line and the slope of the line. A point is already given, (6,2). Now, we must find the slope, m.
Parallel lines always have the exact same slope as the line they are parallel to. So, all we need to do to find the slope of the equation we want is by finding the slope of the first equation. The equation we are given is in standard form, or
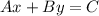 . We can find the slope m from this equation using
. We can find the slope m from this equation using
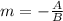 . In
. In
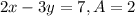 and
and
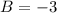 . Thus,
. Thus,
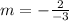 , or just
, or just
 . Now we can begin to plug the numbers into the formula.
. Now we can begin to plug the numbers into the formula.
Point-slope form is written as
 . We can fill in m with the value we found above, as we can fill in
. We can fill in m with the value we found above, as we can fill in
 and
and
 from the given point of (6,2). Filling in the information, we get the equation
from the given point of (6,2). Filling in the information, we get the equation
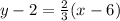 , which simplifies to
, which simplifies to
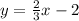 . Either answer usually works, but you should watch out to see if the question asks for a certain form.
. Either answer usually works, but you should watch out to see if the question asks for a certain form.