Question

I tried and I can’t get it

Answer 1

`f(x)=\left \{ {{x+2, x<0} \atop {2 , x\geq0 }} \right.`

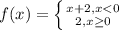
Explanation:

The first equation is one that is true when x<0, so it will be what is to the left of the y-axis. we can find the slope and y-intercept to create the equation, which is easy to see using the graph (mx+b). We can use m = Δy over Δx for slope. The Δy and Δx are both equal to 1, so the slope is 1. The y-int can be seen on the graph at (0,2), so b=2. Plugging in the numbers makes
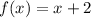`f(x)=x+2`, so x+2 fills in the first box.

For the next piece, we must first define the domain. We can see that it begins at y=0, including (0,2) since the dot is colored in. It moves on infinitely to the right, so we can say that this piece is true when x≥0, which fills in the thrid box. We can find the equation using the same method as before. Starting with the slope, we must find Δy and Δx. This is an oddity, however, since the Δy always equals 0 since the y-value always equals 2. As a result, m=0. The y-intercept can be found on the graph and is still (0,2), so b=2 again. Plugging in the numbers makes
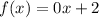`f(x)=0x+2`, which simplifies to
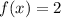`f(x)=2`. Thus, 2 fills the second box.