Question

PLEASE HELP AND SHOW HOW YOU GOT THE ANSWER PLEASEEE

Answer 1

(80)2=((x+2)2+(−8)2)2

Simplify them.

80 = ( {x + 2)}^{2} + 64

80=(x+2)2+64

( {x + 2)}^{2} = 80 - 64

(x+2)2=80−64

( {x + 2)}^{2} = 16(x+2)2=16

( {x + 2)}^{2} = {4}^{2}

(x+2)2=4^2

Cancel square from both sides.

x + 2 = 4

X= 4-2

Therefore, X= 2.

The x-coordinate of B is 2.

Answer 2

Explanation:

Hey there!

The points are; A(-2,3) and B(X,-5). And the distance between them is (√80) units.

We have;

`d = \sqrt{ {(x2 - x1)}^(2) + {(y2 - y1)}^(2) }`

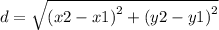
Keep all values.

`√(80) = \sqrt{ {(x + 2)}^(2) + {( - 5 - 3)}^(2) }`

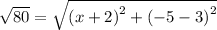
Squaring on both sides.

`{ (√(80)) }^(2) = ( { \sqrt{( {x + 2)}^(2) + ( { - 8)}^(2) } )}^(2)`

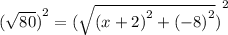
Simplify them.

`80 = ( {x + 2)}^(2) + 64`

`( {x + 2)}^(2) = 80 - 64`

`( {x + 2)}^(2) = 16`

`( {x + 2)}^(2) = {4}^(2)`

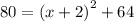
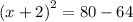
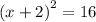
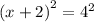
Cancel square from both sides.

`x + 2 = 4`

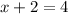
X= 4-2

Therefore, X= 2.

The x-coordinate of B is 2.

Hope it helps....