The 6th term of sequence A is 25, since it's the next perfect square after 16.
The 6th term of sequence B is 9. This sequence is arithmetic with common difference 1, so we just add 1 to the last term to get the next one.
The 6th term of sequence C is 16. Simply subtract the values in the two boxes above (A-B = 25-9 = 16).
----------------------------------------
Note that the general term for sequence A is (n-1)^2. Whatever n is, subtract 1, then square it. For example, if n = 6, then (n-1)^2 = (6-1)^2 = 25.
We're told that 576 is some term and we need to find what term number n.
So,
(n-1)^2 = 576
n-1 = sqrt(576) ... note that
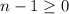
n-1 = 24
n = 24+1
n = 25
So the 25th term is when 576 will show up.