Question

Simplify the following and show the solutions completely.
(x/x+4)–(5/x)​

Answer 1

The following is the expression in simplified form;

`(x)/(x + 4) -(5)/(x) = (x^2 - 5 \cdot x - 20)/(x^2 + 4 \cdot x)`

The solutions are;

x = 5/2 + √(105) or 5/2 - √(105)

Step-by-step explanation:

The given expression is written as follows;

`(x)/(x + 4) -(5)/(x)`

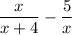
We multiply the denominators to form a common denominator and then multiply each individual fraction numerator by the factor of the common denominator from the other fraction as follows;

`(x)/(x + 4) -(5)/(x) = (x * x - 5 * (x + 4))/((x + 4) * x)`

The above expression is simplified to get;

`(x^2 - 5 \cdot x - 20)/(x^2 + 4 \cdot x)`

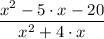
To find the solution of the expression, we equate then expression to zero as follows;

`(x^2 - 5 \cdot x + 20)/(x^2 + 4 \cdot x) = 0`

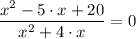
Which gives;

x² - 5·x - 20 = 0 × (x² + 4·x) = 0

x² - 5·x - 20 = 0

Solving with the quadratic equation,
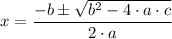`x = \frac{-b\pm \sqrt{b^(2)-4\cdot a\cdot c}}{2\cdot a}` where;

a = 1

b = -5

c = -20

We get;

`x = \frac{5\pm \sqrt{(-5)^(2)-4* 1 * (-20)}}{2* 1} = (5\pm √(105))/(2)`

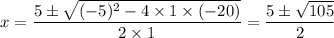
Therefore, the solutions are;

x = 5/2 + √(105) or 5/2 - √(105).