Answer:
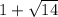
Explanation:
Using pythagorean theorem, x and x+6 are the legs, and x+7 is the hypotenuse.
You can express this as an equation.
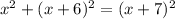
Expanding, this is
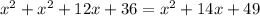
Grouping up, this is
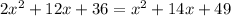
Rearranging, this is
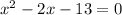
Now, we can use the quadratic formula to solve.
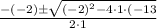 =
=
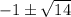 . Since we need x to be positive (due to it being a side length), our answer is
. Since we need x to be positive (due to it being a side length), our answer is
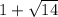 , because it is the positive option
, because it is the positive option