Question

The radius of a sphere is increasing at a rate of 2 inches per minute. Find the rate of change of the volume of the sphere when the radius is 8 inches.

Answer 1

512pi cubic inches a minute

Explanation:

Hello, we would need the volume formula which would be:

V=4/3pi(r)^3

Here we are given the radius is 8 inches and the rate is 2 inches per minute, so we would just plug it in.

`(dV)/(dt) = 4\pi(8)^(3) (2)\\= 8\pi * (8)^(3) \\8^3 =64\\\\8\pi * 64\\\\(dV)/(dt) = 512\pi`

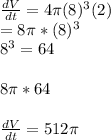
512pi cubic inches a minute would be the answer

Answer 2

512π cubic inches/minute

Explanation:

Volume V = 4/3 π r^3

dV / dr = 4 π r^2

dr/dt = 2

Rate of change of the Volume:

dV/dt = dV / dr * dr/dt

= 4 π r^2 * 2

= 8 π r^2

When r = 8:

dV/dt = 8π(8)^2

= 512π cubic inches/minute