Answer:
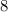 .
.
Explanation:
Notice that in equation for the total dollar amount collected (
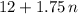 ), every additional bottle sold at the new price brings in
), every additional bottle sold at the new price brings in
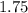 dollars:
dollars:
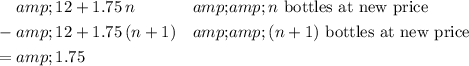 .
.
Therefore, the per-bottle price after the
 price increase would be
price increase would be
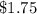 . The per-bottle price before the price increase would be
. The per-bottle price before the price increase would be
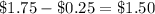 .
.
Also notice that when
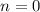 , the total amount collected was
, the total amount collected was
 . In other words, the total amount collected was
. In other words, the total amount collected was
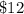 before any bottle was sold at the new price.
before any bottle was sold at the new price.
Thus, the vendor had collected
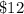 by selling at the initial price of
by selling at the initial price of
 per bottle. The number of bottles sold at that price would be:
per bottle. The number of bottles sold at that price would be:
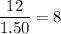 .
.