Answer:
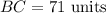
Explanation:
Since AD is an altitude, we know that AD⊥BC by the definition of altitudes.
Then, this means that ∠ADC will be 90° by the definition of perpendicular lines. Therefore:
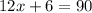
Solve for x. Subtract 6 from both sides and then divide by 12:
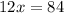
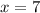
Therefore, the value of x is 7.
BC is the addition of the segments BD and DC. In other words:
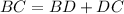
We already know the equations of BD and DC. Substitute:
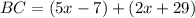
Since we know that the value of x is 7, substitute 7 for x and evaluate for BC:
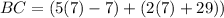
Evaluate:
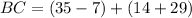
Evaluate:
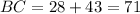
Therefore, the value of BC is 71 units.