Answer:
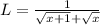
No, It is not true because when x tends to infinity then L tends to 0.
Explanation:
We are given that
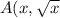 ) and B
) and B
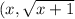 )
)
We have to express distance L between the points A and B as a function of x
and we have to find L tends to infinity when x tends to infinity.
Distance formula between two points is given by
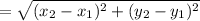
Using distance formula
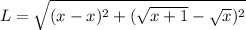
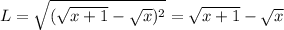
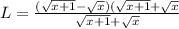
Using rationalization
Now, we get
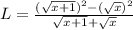
Using identity
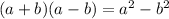
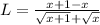
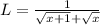
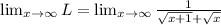
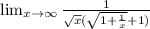
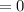
Therefore,when x tends to infinity then L does not tends to infinity.