Question

Express the distance L between the points A(x , √x ) and

B(x, √(x+1)) as a function of x. Is this true L→ ∞ as x→∞ ?

Answer 1

`L=(1)/(√(x+1)+√(x))`

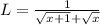
No, It is not true because when x tends to infinity then L tends to 0.

Explanation:

We are given that

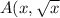`A(x,√(x)`) and B
`(x,√(x+1)`)

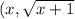We have to express distance L between the points A and B as a function of x

and we have to find L tends to infinity when x tends to infinity.

Distance formula between two points is given by

`=√((x_2-x_1)^2+(y_2-y_1)^2)`

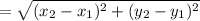
Using distance formula

`L=\sqrt{(x-x)^2+(√(x+1)-√(x))^2}`

`L=\sqrt{(√(x+1)-√(x))^2}=√(x+1)-√(x)`

`L=((√(x+1)-√(x))(√(x+1)+√(x))/(√(x+1)+√(x))`

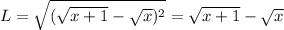
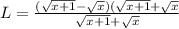
Using rationalization

Now, we get

`L=((√(x+1))^2-(√(x))^2)/(√(x+1)+√(x))`

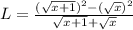
Using identity

`(a+b)(a-b)=a^2-b^2`

`L=(x+1-x)/(√(x+1)+√(x))`

`L=(1)/(√(x+1)+√(x))`

`\lim_(x\rightarrow\infty)L=\lim_(x\rightarrow\infty)(1)/(√(x+1)+√(x))`

`\lim_(x\rightarrow\infty)\frac{1}{√(x)(\sqrt{1+(1)/(x)}+1)}`

`=0`

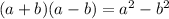
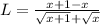
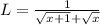
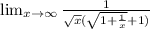
Therefore,when x tends to infinity then L does not tends to infinity.