Answer:
P=0.1227
P=12.27%
Explanation:
Pita has 12 coins in her bag. 3 of those coins are £1 coins and 9 are £0.50.
She takes 3 coins from her bag at random. We want to calculate the probability that she takes exactly £2.50.
To take £2.50, there is only one way to combine three coins:
Two of £1 and one of £0.50
The £1 coins can be extracted from the 3 available
The £0.50 coin can be extracted from the 9 available.
The combination of both events can be calculated as:
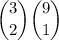
The sample space is the total combination of possible events:
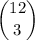
And the probability is:
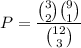
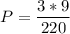
P=0.1227
P=12.27%