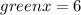∠4x + 29° and angle ∠12x + 55° are interior angles on the same side of transversal . Which means their sum will be equal to 180° .
We can write this in an equation and solve it as :-
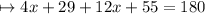

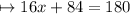
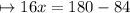
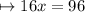
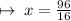
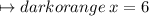
Let us check whether or not we have found out the correct value of x , by placing 6 in the place of x .
So :-
∠4x + 29° :-
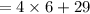

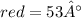
∠12x + 55° :-
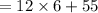
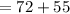

As , 53° + 127° = 180° , we can conclude that we have found out the correct value of x .
Therefore , the value of :-