Question

Working together, it takes two different sized hoses 35 minutes to fill a small swimming pool. If it takes 55 minutes for the larger hose to fill the swimming pool by itself, how long will it take the smaller hose to fill the pool on it's own?

Answer 1

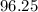`96.25` minutes.

Explanation:

The question states that it takes the larger hose
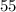`55` minutes to fill the entire pool on its own. Assume that the larger hose fills the pool at a constant rate. What fraction of the pool would this hose fill in each minute?

The larger hose fills
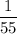`\displaystyle (1)/(55)` of the pool in each minute. That is:
`\displaystyle \frac{1\; \text{pool}}{55\; \rm \text{minutes}} = (1)/(55)\; \text{pool} \cdot \text{minute}^(-1)`.

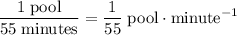Similarly, assume that the smaller hose is also filling the pool at a constant rate. The question states that it takes
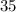`35` minutes for the two hoses to fill the pool when working together. Therefore, when working together, the two hoses would fill
`\displaystyle (1)/(35)` of the pool in each minute. That is:
`\displaystyle \frac{1\; \text{pool}}{35\; \rm \text{minutes}} = (1)/(35)\; \text{pool} \cdot \text{minute}^(-1)`

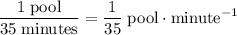
The difference between these two fractions should represent the fraction of the pool that the smaller hose fills in each minute:

The smaller hose fills
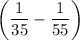`\displaystyle \left( (1)/(35) - (1)/(55) \right)` of the pool in one minute. That's
`\displaystyle \left( (1)/(35) - (1)/(55) \right)\; \text{pool} \cdot \text{minute}^(-1)`.

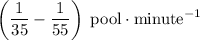At
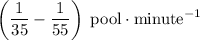`\displaystyle \left( (1)/(35) - (1)/(55) \right)\; \text{pool} \cdot \text{minute}^(-1)`, filling the entire pool would take

`\displaystyle \frac{1\; \text{pool}}{\displaystyle \left( (1)/(35) - (1)/(55) \right)\; \text{pool} \cdot \text{minute}^(-1)} = (1)/(\displaystyle (1)/(35) - (1)/(55))\; \text{minute} = 96.25\; \text{minute}`.

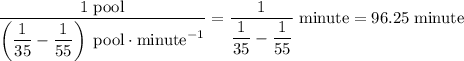Hence, it would take
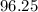`96.25` minutes for the smaller hose to fill the entire pool on its own.