Question

Using the Binomial distribution,

If n=10 and p=0.4, find P(x=5)

Answer 1

P(x=5)=0.2

Explanation:

Binomial Distribution

Consider a random event that has only two possible outcomes. Call p to the probability that the event has a 'successful' outcome, and q to the 'unsuccessful' outcome.

It's clear that p+q=1, or q=1-p.

Now repeat the random event n times. We want to calculate the probability of getting x successful outcomes. This can be done with the following formula:

`\displaystyle P_(x) = {n \choose x} p^(x) q^(n-x)`

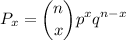
Where

`\displaystyle {n \choose x}`

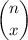
Is the number of combinations:

`\displaystyle {n \choose x} =_nC_x=(n !)/(x ! (n-x) !)`

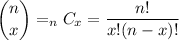
Calculate the probability for n=10, p=0.4, x=5. It follows that q=1-p=0.6:

`\displaystyle P_(5) = {10 \choose 5}\cdot 0.4^(5)\cdot 0.6^(10-5)`

`\displaystyle P_(5) = 252\cdot 0.4^(5)\cdot 0.6^(5)`

`P_(5) = 0.2`

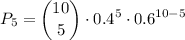
P(x=5)=0.2