We are give with the function:
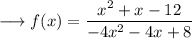
Vertical asymptotes are the points, where the function is not defined, so the denominator must be equal to 0 for making f(x) not defined
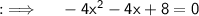
Dividing both sides by -4, we have;
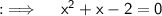
Can be further written as:
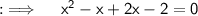
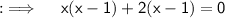
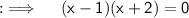
Using zero product rule, Equating both multiplicants to 0, we have:
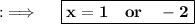
This is the required answer