Question

Unit 1 Scale Drawings Review

(6 OT 6)
This diagram is a scale drawing of a store.
4 inches
1 inches
3 inches
2 inches
Scale: 1 inch - 16 feet
To the nearest 50 square feet, what is the area of the actual store?
A. 2,350 square feet
B. 2,400 square feet
C. 2,450 square feet
D. 2,500 square feet

Answer 1

Correct choice D. 2,500 square feet

Explanation:

Area of a rectangle

The area of a rectangle of dimensions x, y is:

A=x.y

The diagram provided in the question is to a scale of 1 inch=16 ft.

We have provided a modified diagram where all the dimensions are also shown in ft.

The longer side of the shape is 4*16=64 ft

The smaller side of the shape is 3*16=48 ft

The bottom side of the store is 2 1/4*16=36 ft

The leftmost side of the store is 1 3/4*16=28 ft

We need to find the value of x and y.

The value of x is x=64 ft - 36 ft = 28 ft

The value of y is y=48 ft - 28 ft = 20 ft

The area of the whole rectangle of dimensions 48 ft and 64 ft is:

`A1=48 ft * 64 ft = 3,072 \ ft^2`

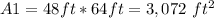
The area of the small blue rectangle is:

`A2=28 ft * 20 ft = 560\ ft^2`

The area of the store is:

`As=A1-A2=3,072 \ ft^2- 560\ ft^2=2,512 \ ft^2`

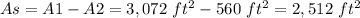
Rounding to the nearest 50 square feet:

`\boxed{As=2,500 \ ft^2}`

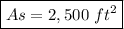
Correct choice D. 2,500 square feet