Given:
Initial population = 4 millions
Growth rate = 7% = 0.07
Present population = 16 millions
To find:
The time it will take for this invasive population to grow from 4 million cane toads to 16 million cane toads.
Solution:
The exponential growth model is
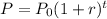
where, P is present population,
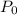 is iniital population, r is growth rate and t is time in years.
is iniital population, r is growth rate and t is time in years.
Substitute P=16,
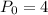 and r=0.07, we get
and r=0.07, we get
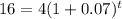
Divide both sides by 4.
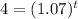
Taking log on both sides.
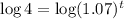
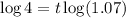
![[\because \log x^n=n\log x]](https://img.qammunity.org/2021/formulas/mathematics/high-school/o9vqwmfsfl6s2ah47gwi871eea8gtbf3hm.png)
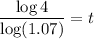
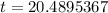
Approx the value to the next integer.
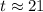
Therefore, the required number of years is 21.