Answer:
Ship 2
Explanation:
From inspection of the diagram, the problem has been modeled as a right triangle. Therefore, to find
 and
and
 , use trigonometric ratios then compare to determine which distance is the smallest.
, use trigonometric ratios then compare to determine which distance is the smallest.
Trigonometric ratios
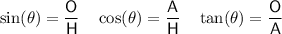
where:
 is the angle
is the angle- O is the side opposite the angle
- A is the side adjacent the angle
- H is the hypotenuse (the side opposite the right angle)
To find
 use the sine trig ratio:
use the sine trig ratio:


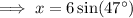

To find
 use the cosine trig ratio:
use the cosine trig ratio:
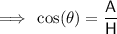
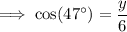
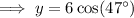
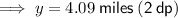
As 4.09 < 4.39, ship 2 is currently closer to the coast guard.