Question

14 . The cost of a mobile phone is pounds

The cost of a television is y pounds
When both prices are increased by £40, the ratio for the cost of the mobile phone to the cost of the television is 15:22
When both prices are decreased by £100, the ratio for the cost of the mobile phone to the cost of the television is 8:15
Find the values of x and y

Answer 1

x= 260, y= 400

Explanation:

Cost of mobile phone= x pounds

Cost of television= y pounds

When both prices are increased by £40,

cost of mobile phone= £(x +40)

cost of television= £(y +40)

`(x + 40)/(y + 40) = (15)/(22)`

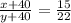
Cross multiply:

15(y +40)= 22(x +40)

Expand:

15y +600= 22x +880

-600 on both sides:

15y= 22x +280 -----(1)

When both prices decreased by £100,

cost of mobile phone= £(x -100)

cost of television= £(y -100)

`(x - 100)/(y - 100) = (8)/(15)`

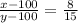
Cross multiply:

15(x -100)= 8(y -100)

15x -1500= 8y -800 (expand)

15x= 8y -800 +1500 (+1500 on both sides)

15x= 8y +700 (simplify)

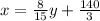`x = (8)/(15) y + (140)/(3)` -----(2)

Subst. (2) into (1):

`15y = 22( (8)/(15) y + (140)/(3) ) + 280`

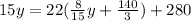
Expand:

`15y = (176)/(15) y + (3080)/(3) + 280 \\ 15y - (176)/(15) y = (3080)/(3) + 280 \\ (49)/(15) y = (3920)/(3) \\ y = (3920)/(3) / (49)/(15) \\ y = 400`

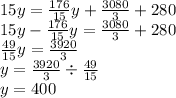
Subst. y=400 into (2):

`x= (8)/(15) (400) + (140)/(3) \\ x = (640)/(3) + (140)/(3) \\ x = (780)/(3) \\ x = 260`