Answer:
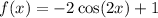
Explanation:
Recall the general cosine equation
- Function:
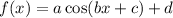
- Amplitude:
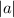
- Period:
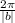
- Vertical Shift:
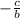
- Midline:
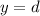
Identify amplitude
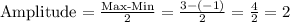
Identify period and solve for b
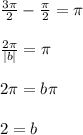
Identify midline

Final Equation
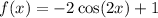
Also, the reason why
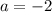 is because a cosine function starts at its maximum, but since it starts at its minimum, the value of
is because a cosine function starts at its maximum, but since it starts at its minimum, the value of
 must be negative and causes the wave to flip about the midline.
must be negative and causes the wave to flip about the midline.