Question

Prove line segment de is congruent to line segment ce

Answer 1

because there is 1 arc on both meaning they are congruent

Explanation:

Answer 2

In trapezium ABCD with diagonals AC and BD intersecting at E, if AD is congruent to BC, and angles BCD and ADC are congruent, then triangles ADE and CBE are congruent by ASA congruence, implying DE is congruent to CE.

To prove that DE is congruent to CE in trapezium ABCD with diagonals AC and BD intersecting at E, we can use the following reasoning:

1. Given Information:

- AD is congruent to BC (Given).

-
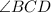`\( \angle BCD \)` is congruent to
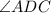`\( \angle ADC \)` (Given).

- Diagonals AC and BD intersect at E in trapezium ABCD (Given).

2. Using ASA Congruence:

- Triangles ADE and CBE share a common side AE (Diagonal).

- AD is congruent to BC (Given).

-
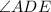`\( \angle ADE \)` is congruent to
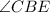`\( \angle CBE \)` (Vertical angles formed by the diagonals).

- By ASA (Angle-Side-Angle) congruence, triangles ADE and CBE are congruent.

3. Corresponding Parts of Congruent Triangles:

- Corresponding parts of congruent triangles are congruent.

- Therefore, DE is congruent to CE as corresponding sides of triangles ADE and CBE.

Thus, DE is congruent to CE in trapezium ABCD given the conditions.