Question

Please show work for the following problem.

In the diagram below, one angle measure is given. Find the measure of each remaining angel, if line l is parallel to line m.

m<1 = ___ Degrees
m<2 = ___ Degrees
m<3 = ___ Degrees
m<4 = ___ Degrees
m<5 = ___ Degrees
m<6 = ___ Degrees
m<7 = ___ Degrees
m<8 = ___ Degrees

Answer 1

`\Large\boxed{m\angle 1 = 110 \textdegree}`

`\Large\boxed{m\angle 2 = 70 \textdegree}`

`\Large\boxed{m\angle 3 = 70 \textdegree}`

`\Large\boxed{m\angle 5 = 110 \textdegree}`

`\Large\boxed{m\angle 6 = 70 \textdegree}`

`\Large\boxed{m\angle 7 = 70 \textdegree}`

`\Large\boxed{m\angle 8 = 110 \textdegree}`

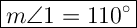
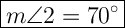
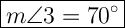
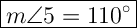
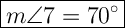
Explanation:

We can use basic angle relationships to find the values of m∠1-8.

Let's first note that line t is being intersected by two parallel lines, L and m. This means that the angles formed by both intersections will be the same.

First off, we know that the 110° is an opposite angle to m∠1. This means their angle measures are the same, so m∠1 is 110°.

We also know that m∠1 and m∠2 are supplementary. This means their angle measures will add up to 180°. This means m∠2 is
`180-110=70 \textdegree`.

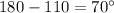m∠2 is also opposite to m∠3. Therefore, their angle measures are the same, and m∠3 = 70°.

Now, we can start thinking about corresponding angles. Basically - what angle formed by line L will correspond to which angle formed by line M?

We can see that m∠2 is corresponding to m∠6. Therefore, their angle lengths are the same, so m∠6 is also 70°.

Now we can use the same logic that we did for line L in line M.

m∠7 and m∠6 are opposite angles, so m∠7 is 70°.

m∠8 is supplementary to m∠6, so m∠8 is
`180-70=110 \textdegree`.

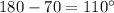m∠5 and m∠8 are opposite angles, so m∠5 is also 70°.

Hope this helped!