Given:
The function is
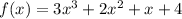
To find:
The value from the given options that is NOT a possible root of the function.
Solution:
According to rational root theorem, all possible roots are in the form of
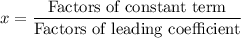
We have,
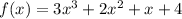
Here,
Leading coefficient = 3.
Constant term = 4
Factors of 3 are ±1, ±3.
Factors of 4 are ±1, ±2, ±4.
Using rational root theorem, all possible roots of given functions are
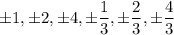
Clearly,
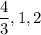 are possible roots but
are possible roots but
 is not the possible root.
is not the possible root.
Therefore, the correct option is C.