Question

A hot air balloon hovers at 92.4 m above the ground. The pilot drops a box over the edge of the basket. How fast does the person standing 10 m away, have to go to catch the box, before it hits the ground?

Answer 1

The person has to move at the speed of 2.30 m/s towards the dropping point to catch the box.

Step-by-step explanation:

Let t be the time taken by the box to reach the ground and v be the speed of the person on the ground standing 10 m away from the dropping

point.

As distance=(speed) x (time), so

`10=vt\cdots(i)`

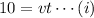
Initially, the height of the box from the ground is 92.4 m.

So, the displacement, s, covered by the box when it reached the ground,

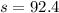`s=92.4` m in the downward direction.

The gravitational force action of the box is also in the downward direction.

The initial velocity of the balloon, u=0.

According to the equation of motion,

`s=ut+\frac1 2 at^2`

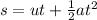
where a is the acceleration, u is initial velocity and.

Here,
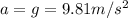`a=g=9.81 m/s^2` (acceleration due to gravity) and s and a are having the same direction.

So, on putting the values in the equation, we have

`92.4=0*t+ \frac 1 2 (9.81)t^2`

`\Rightarrow t^2=(92.4* 2)/(9.81)`

`\Rightarrow t=\sqrt{(92.4* 2)/(9.81)}`

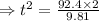
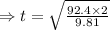
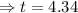`\Rightarrow t=4.34` seconds.

So, the time available for the man on the ground to catch the bot is 4.34 seconds.

Now, from equation (i),

`10=v* 4.34`

`\Rightarrow v = 10/4.34`

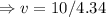
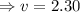`\Rightarrow v = 2.30` m/s.

Hence, the person has to move at the speed of 2.30 m/s towards the dropping point to catch the box.