Question

Juptiter's moon io has a mass of 8.94x10^22 kg and a radius of 1815 km. What is the acceleration due to gravity on the surface of io?

a. 4.33 m/s^2
b. 1.81 m/s^2
c. 2.51 m/s^2
d. 9.81 m/s^2

Answer 1

`g=1.81\ m/s^2`

Step-by-step explanation:

Mass of Jupiter's moon,
`M=8.94* 10^(22)\ kg`

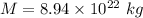
Radius, R = 1815 km

We need to find the acceleration due to gravity on the surface of Juptiter's moon. The formula for the acceleration due to gravity is given by :

`g=(GM)/(R^2)`

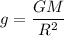
G is universal gravitational constant

`g=(6.67* 10^(-11)* 8.94* 10^(22))/((1815* 10^3)^2)\\\\g=1.81\ m/s^2`

So, the acceleration due to gravity on the Jupiter's moon is
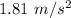`1.81\ m/s^2`.