Question

A Ford is traveling with a velocity of 15m/s, east, and is 200 m ahead of a Chevy traveling in the same direction at 20 m/s. How far will the Chevy travel before catching up to the Ford? Edit: nvm lol I found it

Answer 1

Distance covered by Chevy before catching up to the Ford = 800 meters

Step-by-step explanation:

From the graph attached,

A Ford starts with a velocity = 15 meter per second

Therefore, slope of the line representing the relation between the distance and time =
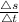`(\triangle s)/(\triangle t)` = Velocity

Let the equation of the blue line,

y = m₁t + b

Where m₁ = slope of the blue line = speed of a Chevy

= 20 meter per second

b = y-intercept

y = 20t + 0 [Since, Chevy starts from the origin, b = 0]

y = 20t

Let quation of the red line,

y = m₂t + b

Where m₂ = Slope of the red line = 15 meter per sec

b = y-intercept = 200 m [Since Ford is 200 meters ahead of Chevy]

y = 15t + 200

Point where these lines will meet or the point where both the cars meet.

20t = 15t + 200

5t = 200

t = 40 seconds

Distance traveled by Chevy in 40 seconds = Velocity × Time

= 20 × 40

= 800 meters per seconds