Question

Several masses m are determined to be equal by comparing them on an equal-arm balance, and a large mass M is found to just balance two of the small ones on a similar balance. The mass M and one of the masses m are each forced to go around a bend of 1.0 m at a constant speed of 1.0 m/s. As they move around the curve their magnitudes of the forces acting on them are

Question 1 options:

a)

equal.

b)

in the ratio of 4:1.

c)

along the direction of motion.

d)

in the ratio of 2:1.

e)

zero.

Answer 1

Option (d) is correct.

Step-by-step explanation:

As the large mass M is found to just balance two of the small mass, m, so

`M=2m\cdots(i)`

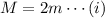
As both the masses M as well as m are forced to go around a bend of 1.0 m at a constant speed of 1.0 m/s.

So, the radius of curvature of the bend (curved path), R= 1.0 m

The speed both the masses, v= 1.0 m/s.

Naturally, without any restriction, all the masses have the tendency to move in a straight line due to its inertia, but here both the masses are moving on the curved path because of the application of the external force on them. This continuous change in the direction is due to the force by the wall of the curved path which is actually the normal reaction by the wall on both the masses.

This reaction force,
`F_R`, balance the centrifugal force, F with which the masses have a tendency to go out of the path, the magnitude of this centrifugal force is,

`F = \frac {mv^2}{R}`

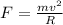
Where m is the mass of the body, v is the speed at that instant, R is the radius of curvature of the path.

So,
`F_R=\frac {mv^2}{R}`

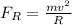
Now, for the small mass, m, the reaction force on it is

`F_R1= \frac {mv^2}{R}`

`\Rightarrow F_R1= \frac {m(1)^2}{1}`

`\Rightarrow F_R1= m \cdots(ii)`

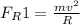
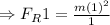
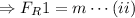
And for the bigger mass, M, the reaction force on it is

`F_R2= \frac {Mv^2}{R}`

`\Rightarrow F_R2= \frac {M(1)^2}{1}`

`\Rightarrow F_R2= M`

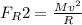
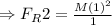
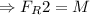
By using equation (i), we have

`F_R2= 2m`

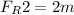
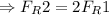`\Rightarrow F_R2=2F_R1` [by using (ii)]

`\Rightarrow F_R2 / F_R1 = 2/1`

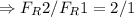
So, the ratio of force acting on the bigger mass M to the magnitude of the force acting on the smaller mas m is 2:1.

Hence, option (d) is correct.