Question

Find the relative rate of change at the given value of . Assume is in years and give your answer as a percent

Answer 1

84.37 %.

Explanation:

The question is shown in the attached figure.

We have,

`f(t)=2t^3+10,\ t=3`

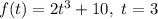
We can find the value of f(t) at t = 3,

`f(3)=2(3)^3+10\\\\f(3)=64`

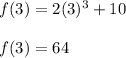
Finding f'(t).

`f'(t)=6t^2`

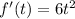
Finding f'(t) at t = 3

`f'(3)=6(3)^2\\\\=54`

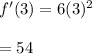
The relative change is calculated as :

`(f'(t))/(f(t))=(54)/(64)\\\\=0.8437`

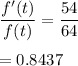
In percentage rate of change,

`(f'(t))/(f(t))=0.8437* 100\\\\=84.37\%`

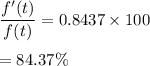
Hence, the required percent change is 84.37 %.