Answer:
Vertex (4.53 , 335.33) Zeroes are -0.048 and 9.11
Explanation:
For find the Vertex also know as the turning point/stationary point and the zeros also known as the x-intercepts of the equation we equate the equation to its complete square form which is

where (h,k) are the vertex point of the equation h corresponds to x coordinate and k corresponds to the y coordinate and a determines whether the graph is a maximum or a minimum. To find whether the graph is a maximum value of a should be < 0 which and if a's value is > 0 then the graph is a minimum. In short
 maximum (n shaped)
maximum (n shaped)
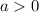 minimum (u shaped
minimum (u shaped
so now we equate, that is
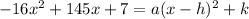
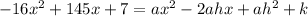
now we compare the coefficients of x^2
-
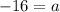
now we compare the coefficients of x
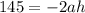
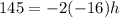
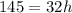
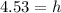
now we compare constants
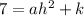

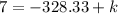

so now we the value of (h , k) that is (4.53 , 335.33)
that is our vertex and since the value of a is less than zero the graph is a maximum.
Now for the zeroes/x-intercepts
we need to find where the graph cuts the x-axis which means if the specific point where the curve cuts the x-axis that point's y coordinate should be zero or more like
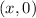 .
.
and thus this point lies on the curve/equation as well because it satisfies it which means we can put this point into our given equation
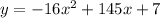 when we put
when we put
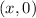 in it y becomes 0 thus changing it to
in it y becomes 0 thus changing it to
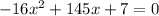
this becomes a simple quadratic equation where we can use the quadratic formula
 ±
±
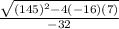
we get two values of x
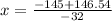 and
and
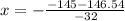
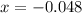 and
and
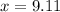 since there 2 values of x means the curve cuts the x-axis at two points we can even confirm our answers by using the desmos graphing calculator as well to check our vertex and zeroes.
since there 2 values of x means the curve cuts the x-axis at two points we can even confirm our answers by using the desmos graphing calculator as well to check our vertex and zeroes.