Question

A student graphs the functions f(x) = | x+3 | and g(x) = x2-2x+3 on the coordinate plane shown.

Which are the solutions of f(x) =g(x)?

A. -3 and 1

B. -1 and 1

C. 0 and 3

D. 3 and 6

Answer 1

The solutions are the intersection point of both graphs

• The left side graph is y=|x+3|
• The right side top graph is x²-2x+3(Parabola)

So there mUST be two solutions

The intersections are

• (0,3)
• (3,6)

The x values are solution

• They are 0,3

Option C

Answer 2

C. 0 and 3

Explanation:

The solutions of f(x) = g(x) are the values of the x-coordinates of the points where the two graphed functions intersect.

From inspection of the graph, the points of intersection are:

• (0, 3)
• (3, 6)

Therefore, the solutions are 0 and 3 (since they are the x-values).

Proof

`\implies f(x) = g(x)`

`\implies |x + 3| = x^2-2x+3`

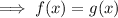
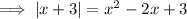
We only need to take the positive form of |x+3| since we can see from the graph that g(x) intersects f(x) when |x+3| is positive:

`\implies x + 3 = x^2-2x+3`

`\implies x^2-3x=0`

`\implies x(x-3)=0`

`\implies x=0, 3`

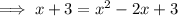
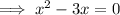
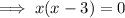
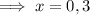
Thus confirming that the solutions are when x = 0 and 3