Question

You throw a ball up to a friend who is on a balcony 38 ft above the ground. You throw the ball with a starting velocity of 48 ft/s. The ball is 6 ft high when it leaves your hand. After how many seconds will your friend have a chance to catch the ball? Use the vertical motion formula

Answer 1

Our friend will have two chances to catch the ball: (i) 1.005 seconds after launch, (ii) 1.978 seconds after launch.

Explanation:

In this case, we see that ball is launched up in free fall motion, which is an uniform accelerated motion in which ball is accelerated by gravity and effects of air friction and Earth's rotation are neglected. We have to find how many time our friend would need to wait to have a chance to catch the ball. The height of the ball is represented by this equation of motion:

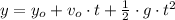`y = y_(o)+v_(o)\cdot t + (1)/(2)\cdot g \cdot t^(2)` (Eq. 1)

Where:

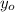`y_(o)` - Initial height of the ball, measured in meters.

`y` - Final height of the ball, measured in meters.

`v_(o)` - Initial velocity of the ball, measured in meters per second.

`g` - Gravitational acceleration, measured in meters per square second.

`t` - Time, measured in seconds.

If
`y_(o) = 6\,ft`,
`y = 38\,ft`,
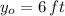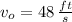`v_(o) = 48\,(ft)/(s)` and
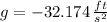`g = -32.174\,(ft)/(s^(2))`, we solve the resulting expression for
`t`:

`-16.087\cdot t^(2)+48\cdot t -32 = 0`

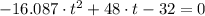
Roots are found by Quadratic Formula:

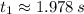`t_(1)\approx 1.978\,s` and
`t_(2) \approx 1.005\,s`

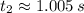
First root represents the instant after reaching maximum height, while the second one is for the instant before reaching that height. Hence, our friend will have two chances to catch the ball: (i) 1.005 seconds after launch, (ii) 1.978 seconds after launch.