Answer:
The frequency of rotation of the platform is approximately 27.970 revolutions per minute.
Step-by-step explanation:
In this case, the astronaut experiments a centrifugal acceleration as a reaction to the centripetal acceleration due to the rotation of the platform. (Second and Third Newton's Laws). Centripetal acceleration (
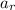 ), measured in meters per second, is expressed as:
), measured in meters per second, is expressed as:
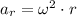 (Eq. 1)
(Eq. 1)
Where:
 - Angular velocity, measured in radians per second.
- Angular velocity, measured in radians per second.
 - Distance of the astronaut's feet from the rotational axis of the platform, measured in meters.
- Distance of the astronaut's feet from the rotational axis of the platform, measured in meters.
Now we clear the angular velocity:
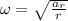
If we know that
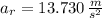 and
and
 , the angular velocity of the platform is:
, the angular velocity of the platform is:

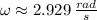
And this outcome is converted into revolutions per minute:

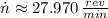
The frequency of rotation of the platform is approximately 27.970 revolutions per minute.