Answer:
As the sample size is large enough, i.e. n = 198 > 30 the central limit theorem can be applied to describe the sampling distribution for the sample proportion of children who are nearsighted.
Explanation:
Let the random variable p denote the proportion of children affected by nearsightedness.
The previously known proportion was, p = 0.12.
A random sample of n = 198 children are selected.
According to the Central limit theorem, if from an unknown population large samples of sizes n > 30, are selected and the sample proportion for each sample is computed then the sampling distribution of sample proportion follows a Normal distribution.
The mean of this sampling distribution of sample proportion is:
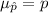
The standard deviation of this sampling distribution of sample proportion is:
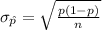
As the sample size is large enough, i.e. n = 198 > 30 the central limit theorem can be applied to describe the sampling distribution for the sample proportion of children who are nearsighted.