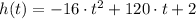Answer:
The equation that best models the height of Elena's rocket is
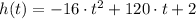
Explanation:
Let
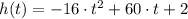 , where
, where
 is the height of the rocket, measured in feet, and
is the height of the rocket, measured in feet, and
 is the time, measured in seconds. From Mechanical Physics, we notice that such second order equation represents a free fall movement, which is a type of uniform accelerated motion, in which rocket is accelerated by gravity and effects from air friction and Earth's rotation are considered negligible.
is the time, measured in seconds. From Mechanical Physics, we notice that such second order equation represents a free fall movement, which is a type of uniform accelerated motion, in which rocket is accelerated by gravity and effects from air friction and Earth's rotation are considered negligible.
The general equation for the height of the rocket is:
 (Eq. 1)
(Eq. 1)
Where:
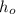 - Initial height of the rocket, measured in meters.
- Initial height of the rocket, measured in meters.
 - Initial velocity of the rocket, measured in meters per second.
- Initial velocity of the rocket, measured in meters per second.
 - Gravitational acceleration, measured in meters per square second.
- Gravitational acceleration, measured in meters per square second.
In US units, gravitational acceleration equals 32.174 feet per square second and indicates that rocket is decelerated by gravity.
The first grade monomial inside the polynomial contains the initial velocity of the rocket and the zero grade monomial represents the initial height of the rocket.
If Elena launches her rocket from the same position but with an initial velocity double that of velocity of Justin's rocket, then, the equation that best models the height of Elena's rocket is: