Answer:
The selling price of each widget is 15.63 cents.
Explanation:
A quadratic function or function of the second degree is a polynomial function of the form:
f(x)= a*x² + b*x + c; or y=a*x² + b*x + c
The maximums and minimums in a function f are the largest (maximum) or smallest (minimum) values or extremes that the function takes. The vertex is a point that is part of the parabola that coincides with the maximum or minimum of the function:
- if a is greater than 0, being positive, the vertex of the parabola is at the bottom of it, being a minimum (that is, the parable opens "up").
- if a is less than 0, being negative, the vertex is at the top, being a maximum (that is, the parabola opens "down").
In this case you know that the amount of profit, y, made by the company is related to the selling price of each widget, x, by:
y= -44*x²+1375*x-6548
In this case, comparing with the form of the quadratic function:
So, since the value of a is less than zero, the vertex will be the maximum of the function. Therefore, the vertex will indicate the price at which the devices should be sold for the company to obtain the maximum profit.
The value of the vertex on the abscissa axis (the x-axis) is:
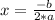
In this case:
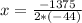
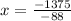
x= 15.63
Since x represents the selling price of each widget, then this will be 15.63 cents.