Question

The generator in a purely inductive AC circuit has an angular frequency of 553 rad/s. If the maximum voltage is 222 V and the inductance is 0.102 H, what is the rms current in the circuit? Answer in units of A

Answer 1

The rms current is 2.78 A

Step-by-step explanation:

Given;

angular frequency, ω = 553 rad/s

maximum voltage, V₀ = 222 V

inductance, L = 0.102 H

The inductive reactance is given by;

`X_l = \omega L\\\\X_l = 553 *0.102\\\\X_l = 56.406 \ ohms`

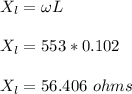
The root mean square voltage is given by;

`V_(rms) = 0.7071 \ V_o\\\\V_(rms) = 0.7071 * 222\\\\V_(rms) = 156.976 \ V`

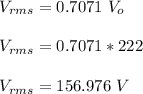
The rms current is given by;

`I_(rms) = (V_(rms))/(X_l) \\\\I_(rms) = (156.976)/(56.406)\\\\ I_(rms) = 2.78 \ A`

Therefore, the rms current is 2.78 A