Question

The pH of a solution of 4-chlorobutanoic acid is measured to be . Calculate the acid dissociation constant of 4-chlorobutanoic acid. Round your answer to significant digits.

Answer 1

`Ka=2.99x10^(-5)`

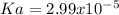
Step-by-step explanation:

Hello.

In this case, as you are not indicating the molarity of the solution and its pH we are going to assume they are 1.4 M and 2.19 respectively as typical problems over this. In such a way, based on the pH we can compute the concentration of hydrogen ions in the solution:

`[H^+]=10^(-pH)=10^(-2.19)=6.467x10^(-3)M`

Next, the dissociation of 4-chlorobutanoic acid is:

`Cl-CH_2-CH_2-CH_2-COOH\rightleftharpoons H^++Cl-CH_2-CH_2-CH_2-COO^-`

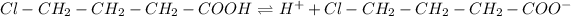
Since it is a weak acid, therefore, its equilibrium expression is:

`Ka=([H^+][Cl-CH_2-CH_2-CH_2-COO^-])/([Cl-CH_2-CH_2-CH_2-COOH])`

Since the concentration of hydrogen ions equal the concentration of 4-chlorobutanoate ions at equilibrium and the concentration the 4-chlorobutanoic acid equals 1.4 M minus the concentration of hydrogen ions, which is related to the reaction extent
`x`, the acid dissociation constant is:

`Ka=(6.467x10^(-3)*6.467x10^(-3))/(1.4-6.467x10^(-3))\\ \\Ka=2.99x10^(-5)`

Best regards!