Answer:
C. 0 and 3
Explanation:
The solutions of f(x) = g(x) are the values of the x-coordinates of the points where the two graphed functions intersect.
From inspection of the graph, the points of intersection are:
Therefore, the solutions are 0 and 3 (since they are the x-values).
Proof

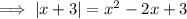
We only need to take the positive form of |x+3| since we can see from the graph that g(x) intersects f(x) when |x+3| is positive:

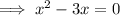
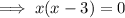
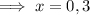
Thus confirming that the solutions are when x = 0 and 3