Question

ou invest $1000 in a mutual fund. You expect that the fund will earn a 8% return annually before expenses (~this is how much the fund's assets go up). You have a choice between purchasing class A mutual fund shares with a front-end load of 4% and no expenses or class C mutual fund shares with no loads but a 1% 12b-1 fee. What is your investment horizon if you are indifferent between these two

Answer 1

4.3883 years

Step-by-step explanation:

The investment horizon to be indifferent between both investments is the number of years it takes for the total investment sum + interest on both investments to be the same. If that value is 'n', then

the value of class A mutual fund at n years =
`1000(1-0.04)*(1.08)^(n)`

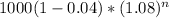
the value of class C mutual fund after n years =
`1000*(1.08-0.01)^(n)`

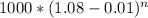
At the point of indifference, the values of both investments will be the same.

Therefore,

`1,000(1-0.04)(1.08)^(n) =1,000(1.08-0.01)^(n) \\960*(1.08)^(n) =1,000*1.07^(n)\\(1.08^(n) )/(1.07^(n)) =(1,000)/(960)\\((1.08)/(1.07))^(n) =1.041667\\1.009346^(n) =1.041667\\n=4.3883`

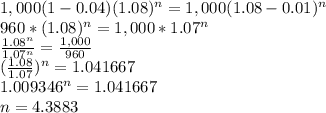
This is the value of n that solves the equation (deduced by interpolation).

Therefore the investment horizon of indifference = 4.3883 years.