Answer:
The speed of body B after collision is 128 cm/s
Step-by-step explanation:
Given;
initial speed of body A,
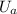 = 80 cm/s (forward direction)
= 80 cm/s (forward direction)
initial speed of body B,
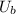 = - 40 cm/s (backward direction)
= - 40 cm/s (backward direction)
mass of body A,
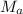 = 140 g
= 140 g
mass of body B,
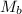 = 60 g
= 60 g
let the speed of body A after collision =
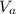
let the speed of body B after collision =
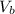
Apply the principle of conservation of linear momentum;
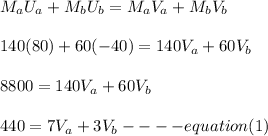
One direction velocity;
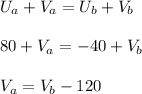
substituting the value of Va in the first equation, we will have;
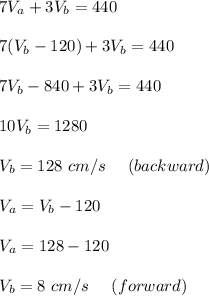
Therefore, the speed of body B after collision is 128 cm/s