Answer:
The time when the swim team member is 5 feet above the water surface is 7.4 seconds.
Explanation:
You want to know when a member of the swim team finished his jump no later than 5 feet above the surface of the water to prepare for the splash, that is, when t is 5 feet above the surface of the water. Substituting h(t) for this value 5 in the equation you obtain:
5= -0.875*t²+5.25*t+14
A quadratic equation has the general form:
a*x² + b*x +c= 0
where a, b and c are known values and a cannot be 0.
Taking the equation 5= -0.875*t²+5.25*t+14 to that form, you get:
-0.875*t²+5.25*t+14-5=0
-0.875*t²+5.25*t+9=0
The roots of a quadratic equation are the values of the unknown that satisfy the equation. And solving a quadratic equation is finding the roots of the equation. For this you use the formula:

In this case, solving the equation is calculating the values of t, that is, you find the time when the swim team member is 5 feet above the water surface.
Being a= -0.875, b=5.25 and c= 9, then
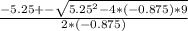
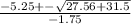

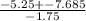
Then:
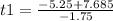 and
and
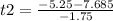
Solving for t1:
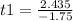
t1= -1.39 ≅ -1.4
Solving for t2:

t2= 7.39 ≅ 7.4
Since time cannot be negative, the time when the swim team member is 5 feet above the water surface is 7.4 seconds.